Mathematical ideas behind variant calling

So you’re staring at IGV and you are convinced you can see a variant is present? There are a half a dozen reads out of a thousand that support the variant, in line with your expectations of the variant frequency. How confident are you that the variant is truly contained in the sample?

In DNA sequencing, every read carries a chance of containing random error. This simple fact sets limits on our ability to detect true variants, especially when they are present at low allele frequencies.

The link is immediate and obvious: if the random error rate of sequencing reads is, say, 0.5%, then any true somatic variant appearing at 0.5% frequency will be buried in a sea of errors. The signal and the noise are of the same magnitude: distinguishing real variants from errors becomes fundamentally fraught with uncertainty.

Even for higher allele frequencies, the error rate dictates the sensitivity. If a variant is present at 1% and the read error rate is 0.1%, then a significant fraction of what looks like variation could still be noise. Detection becomes a statistical problem: the variant signal must statistically exceed the background of errors. Even in the case of inherited variants, where a variant is present in all cells and the frequency is either 100% (homozygous) or 50% (heterozygous), ambiguity remains.

In this article, we will explore the mathematics of variant calling, and how the error rate of sequencing reads can affect our ability to detect true variants. Although many people are aware of the problem, and the general gist of the arguments above, our ability to confidently detect variants is often overestimated. By working through a simple mathematical model, we will show how the error rate can overwhelm the signal of true variants, and how this makes it difficult to detect low-frequency variants. The major practical consequence of the discussion is setting the right expectations for our ability to confidently claim that a variant is present.

For a variant allele frequency of 0.3%, an error rate of 0.2%, and a prior probability of a variant being present of 0.1%, the observation of 5 out of 1000 supporting reads provides only 0.49% confidence that a variant is present.

The beginnings of a solution

A naive, but principled, variant caller could use Bayes’ theorem to attempt detection. Bayes’ theorem is the basis of much of modern statistics and machine learning. It is a simple rule for updating what you believe when you see new evidence. It tells you how to combine your prior belief about something with how likely the new data is, to get a new, updated belief. The rule can be used recursively, so that you can keep updating your beliefs as you see more and more data. In the context of variant calling, it can be used to combine observations from many sequencing reads to understand where a variant is likely to be present. In short: it’s a way to turn observations into stronger or weaker confidence, depending on how surprising the evidence is.

Given an observed number of variant-supporting reads, the naive caller could compute the posterior probability that a true variant exists, versus the probability that the observation arose purely from random errors. In its most basic form:

$$ P(\text{Variant} | \text{Data}) \propto P(\text{Data} | \text{Variant}) \times P(\text{Variant}) $$

This expression states that the probability of a variant being present given the data (P(Variant | Data)) is proportional to the probability of seeing the observed data if a variant is present (P(Data | Variant)) multiplied by the prior probability of a variant being present (P(Variant)). (The proportionality constant is the total probability of the data, which serves to normalise the quantity shown above). The term on the left is called the posterior probability; it is derived after seeing the data. The prior probability, P(Variant), by contrast is known prior to observing data. The other term on the right, P(Variant | Data), is called the likelihood. For now it is not important how we calculate the likelihood, the important part is how the right-hand side of the equation is constructed as a likelihood multiplied by a prior. The likelihood describes how likely the data is under two different assumptions: that a variant is present, and that it is not.

The important part

So the likelihood P(Data | Variant) reflects the likelihood of seeing the observed reads, if a real variant is present. Typically the likelihood is high if the variant frequency is high, and reads contain few errors (so variants are observed in many reads). Intuitively, if a variant is present at 50% allele frequency, then half of the reads will show evidence for it. If the variant is present at 1%, then only 1 in 100 reads will show evidence for it.

However, these statements must be understood in the limit of observing an infinity of reads. When we observe a finite number of reads, the likelihood is not just a function of the variant frequency. Later we will go on to calculate what exactly can be deduced from observing a variant in 1% of reads.

An observation of a variant in 1% of reads does not mean that the variant is present at 1% frequency.

For now let us consider a second likelihood: P(Data | No Variant). This one reflects the likelihood that no variant is present --- that is that any non-reference bases in individual reads are errors, not true variants. It is clear that if we observe data containing a variant, but the true situation is that no variant is present, then this likelihood can only be non-zero if the reads are not perfect. Analogous and in opposition to P(Data | Variant), this second P(Data | No Variant) likelihood is naturally high when variant frequency is low. However, it can also be high when the true variant frequency is low, and the error rate is non-zero and on the order of the variant frequency.

This is the crux of the problem: if the error rate is high enough, then the likelihood of seeing a variant in 1% of reads can be high even when the true variant frequency is much lower than 1%. The Bayesian framework does not solve a fundamental issue. It can help prioritize calls, but it cannot create information where none exists. True variants may slip through undetected when they cannot overcome the background error rate. Worse still, false positives (random noise masquerading as real variation), will clutter results. Interpretation becomes chaotic when every low-frequency variant call is suspect.

Being more quantitative

The arguments above are a good start, but they are qualitative. The likelihoods are not just functions of the variant frequency, but also depend on the number of reads, the error rate, and the distribution of errors. This is where our intuition can fail us. A combination of factors can lead to a situation where the likelihood of seeing a variant in 1% of reads is high, even when the true variant frequency is much lower than 1%.

In the following sections we will explore the mathematics of this situation in more detail. We will start with a simple model of sequencing reads, and then we will explore how the likelihoods are constructed. Our simple model serves to illustrate this basic idea that evidence for variants, particularly when the true variant frequency is low, can be overwhelmed by random errors. And, that it is overwhelmed far more quickly than many people intuitively expect.

A simple model

To be more quantitative, we can model sequencing read counts using binomial distributions. Each read is an independent Bernoulli trial: either it supports the variant, or it does not. Don’t worry about the terminology: these are just names for simple, familiar ideas.

Suppose we have:

• a total reads of $n$ covering a locus,
• the true variant allele frequency (VAF) is $p$ if a variant exists, and
• the error rate $e$ is the probability that a read erroneously contains the variant allele.

Then the number of variant-supporting reads, $k$, we observe when no variant is present can be calculated as:

$$ P(k \mid \text{No Variant}) = \binom{n}{k} e^k (1-e)^{n-k} $$

This formula comes from the binomial distribution, which models the number of successes in a fixed number of independent trials. In the sequencing context, each read is an independent trial with two possible outcomes: it either erroneously supports the variant with probability $e$, or it does not with probability $1 - e$. The first term, binomial coefficient, counts how many ways $k$ variant-supporting reads can occur among a list of $n$ total reads. The two exponential terms then give the probability of any one such arrangement; the first exponential term relates to the $k$ variant-supporting reads, and the second relates to observing the remaining $n - k$ non-variant-supporting reads. Multiplying everything together gives the overall probability of observing exactly $k$ variant reads out of $n$, assuming a variant is not present.

The binomial distribution models the outcome of repeating many independent yes/no experiments, where each experiment succeeds with the same probability.

We can also calculate the probability of observing $k$ variant-supporting reads under the assumption that a variant is indeed present:

$$ P(k \mid \text{Variant}) = \binom{n}{k} p_v^k (1-p_v)^{n-k} $$

This is analogous to the previous equation except we have replaced $e$ with $p_v$ :

$$ p_v = p(1-e) + (1-p)e $$

This is the probability of observing a variant-supporting read when a variant is present, including the possibility that some of the reads erroneously support the variant. Note that when both $e$ and $p$ are small, this is approximately equal to their sum.

It is somewhat standard in these models to lump together the error rate and the variant frequency and consider $p_v$ to be a free parameter. We would then describe the model as $p_v$ being the probability of observing a variant-supporting read when a variant is present, and $e$ as the probability of observing a variant-supporting read when no variant is present. The change makes the equations below easier to follow, and so we will use $p_v$ throughout. But just remember that $p_v$ is a function of both the variant frequency and the error rate --- it is not simply the variant probability, but includes the error rate as well.

For completeness, and because it’s something you’ll often hear discussed, we’ll introduce the ratio:

$$ \text{LR} = \frac{P(k \mid \text{Variant})}{P(k \mid \text{No Variant})} $$

This is the likelihood ratio (LR) for observing $k$ variant-supporting reads. A large likelihood ratio supports the presence of a true variant; a small one supports no variant.

If all of that was a bit much, don’t worry, we now have all we need to calculate interesting quantities. The rest of the maths in this article is just algebraic manipulation of the above equations.

Does 0.3% variant-supporting reads mean a variant is present, with a frequency of 0.3%?

With this modicum of maths under our belt, we can calculate the likelihood ratio in a simple example. Suppose we have 1000 reads, and we observe 5 variant-supporting reads. Let us assume a sequencing error rate of 0.2% ($e = 0.002$).

We can calculate the variant likelihood as:

$$ P(k=5 \mid \text{Variant}) = \binom{1000}{5} p_v^5 (1-p_v)^{995} $$

and similarly the no-variant likelihood as:

$$ P(k=5 \mid \text{No Variant}) = \binom{1000}{5} e^5 (1-e)^{995} $$

Substituting the values of p_v and e into the equations above gives us:

$$ P(k=5 | \text{Variant}) = 17.6\% $$ $$ P(k=5 | \text{No Variant}) = 3.6\% $$

This gives us a likelihood ratio of around 5. So although the likelihood of observing 5 variant-supporting reads is higher if a variant is present, it is not overwhelmingly so. (This doesn’t mean there is an 80% chance the variant is present, it just means that the likelihood of observing 5 reads is 5 times more likely if a variant is present than if it is not).

Herein lies the problem. Let’s remember back to Bayes’ theorem. The posterior probabilites we want, P(Variant | Data) and P(No Variant | Data), are proportional to the likelihoods we have just calculated, but they also include the prior probabilities. These prior probabilities can dominate the posterior probabilities.

If we assume a prior probability of 0.1% for the variant being present, then we can calculate the posterior probability of the variant being present given the observation of 5 variant-supporting reads:

$$ \begin{align} P(\text{Variant} \mid \text{Data}) &= \frac{0.001 \times 0.176}{0.001 \times 0.176 + 0.999 \times 0.036} \ &= 0.49 \% \end{align} $$

(note here we have used the full Bayes’ theorem, which includes the total probability of the data in the denominator). While 5 supporting reads match the expected number for a 0.3% true variant (the allele frequency plus expected erroneous observations), it is not uniquely diagnostic because random sequencing errors can also produce similar counts in the absence of a true variant. Let this sink in:

1. Despite observing the expected value for the number of supporting reads for a variant at 0.3% frequency,
2. and the likelihood ratio being around 5,
3. the probability of a true variant being present is only 0.49%,
4. because the prior probability of a variant being present is so low.

Whilst it is not surprising that observing variant-supporting reads at the expected level when the error rate is a similar level, does not provide strong evidence for a variant being present, it is perhaps surprising just how weak the evidence is. The issue is exacerbated by the fact that the prior probability of a variant being present is often very low. The value of 0.1% used here is in fact quite high for the situation of somatic variation, where the prior probability of a variant being present would be more like 10^-6.

To further solidify this point, we can calculate the posterior probability of a variant being present for a range of supporting variant reads. For this, we simply run through the calculation above swapping out the value of $k$, with a range of values. The result is Figure 1. A counterintuitive result here is how many variant supporting reads are needed to get a posterior probability of 50% or more. The crossing point is around 11 variant-supporting reads. This is almost four times the expected number of reads for a variant present with a VAF of 0.3%. Of course a component of this reflects the 0.2% error rate. While intuition might suggest 5 reads is enough (matching the expected variant frequency), the mathematics shows we required more evidence. To get a posterior probability of 95% or more that a variant is present, we need around 15 variant-supporting reads. This is a significant number of reads, and it is easy to see how the prior probability can dominate the posterior probability.

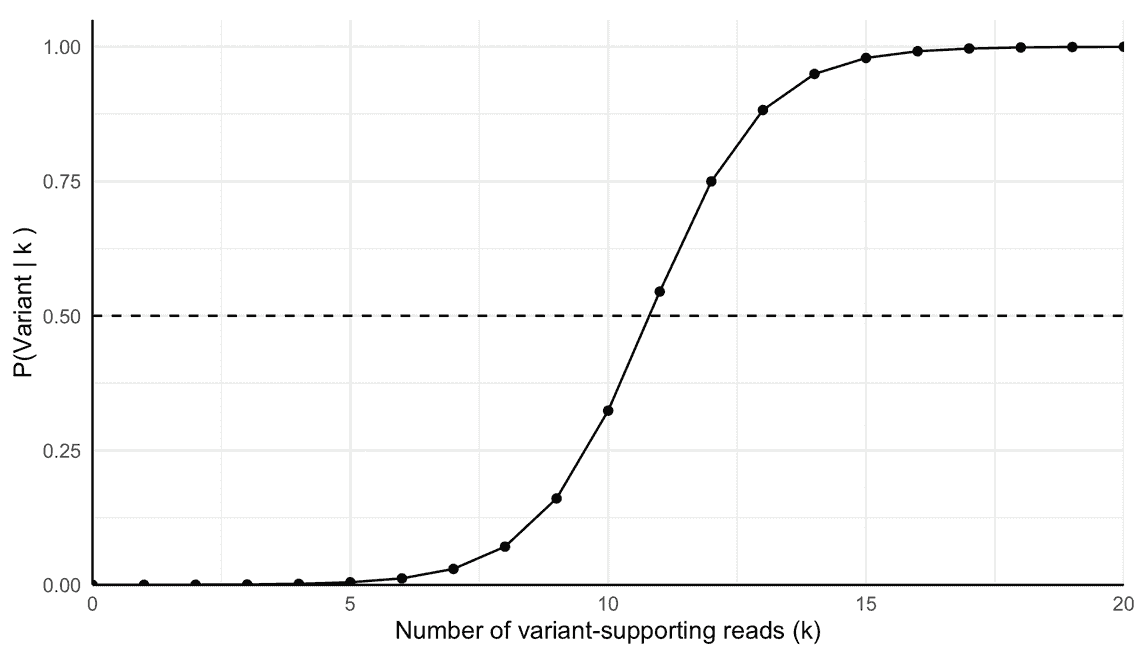
How do we detect low frequency variants?

In the previous section we saw our ability to detect low frequency variants can be dominated by the prior probability of a variant being present. As presented, it all seems a bit gloomy, so the natural question is how do we detect low frequency variants?

There’s a blindingly obvious answer: increase the number of reads. We may have thought that 1000 reads was a lot, but in fact it is not. Particularly when we consider the other parameters of importance: the variant frequency, the error rate, and the prior probability that a variant is present.

There’s a large space to explore here, but let’s consider the question: “how many reads do we need to observe a variant at 0.3% frequency with 95% confidence, when the error rate is 0.2% and the prior probability of a variant being present is 0.1%“. We can calculate this using the same methods as above.

First let’s establish what we mean by “95% confidence”. This means that we want the posterior probability of a variant being present to be 95% or more. i.e. that P(Variant | Data) > 0.95, or equivalently the odds ratio of the posterior probability to the prior probability is greater than 19. We can rewrite Bayes’ theorem in an odds ratio form. The odds of an event is the ratio of the probability of the event occurring to the probability of it not occurring: odds = P(event) / (1 - P(event)). So Bayes’ theorem can be rewritten as:

$$ \text{Posterior Odds} = \text{Prior Odds} \times \text{Likelihood Ratio} $$

where: $$ \text{Posterior Odds} = \text{“confidence”} / (1 - \text{“confidence”}) = 19 $$ $$ \text{Prior Odds} = P(\text{Variant}) / P(\text{No Variant}) = 0.001 / 0.999 $$

and the likelihood ratio is as defined above. Our expression for the likelihood ratio is (with the binomial coefficients cancelling out):

$$ \text{Likelihood Ratio} = \frac{P(k \mid \text{Variant})}{P(k \mid \text{No Variant})} = \frac{p_v^k (1-p_v)^{n-k}}{e^k (1-e)^{n-k}} $$

This is a bit of a mouthful, but it is not too bad. Combining everything together, and allowing $k = vn$, where $v$ is the variant frequency and $n$ is the number of reads, we can rearrange to give us:

$$ n = \frac{ \log\left( \frac{\text{Posterior Odds}}{\text{Prior Odds}} \right) }{ v \log A + (1-v) \log B } $$

where:

$$ A = \frac{p}{e} $$ $$ B = \frac{(1-p)}{(1-e)} $$

and where we choose the posterior odds by our desired confidence level, and choose prior odds by our prior probability of a variant being present, i.e. P(Variant) / P(No Variant).

If we plug in all our numbers for this we end up with the following. Note we kept $p_v$ and v separate in the above but here we can set them equal, since we are looking for the number of reads needed to detect a variant at the expected variant frequency. The value 0.004988 corresponds to $p_v$ with $p$ = 0.003 and $e$ = 0.002 (see the note above about how $p_v$ can be decomposed).

$$ n = \frac{ \log (\frac{19}{0.001 / 0.999}) } { 0.004988 \log \frac{0.004988}{0.002} + (1 - 0.004988) \log \frac{(1-0.004988)}{(1-0.002)}} = 6254 \text{ reads} $$

So not a huge number of reads, but a significant increase from the 1000 we started with. The equation above provides a general way (albeit from a simple model) to calculate the number of reads needed to detect a variant at a given frequency with a given confidence. We can check the result by taking 6254 and 6254 x $p_v$ = 31 and putting these into our earlier equations. Doing so correctly leads to a posterior probability of ~94.1%, close to the 95% we targeted and much larger than the paltry 0.49% we started with. This is shown in Figure 2.

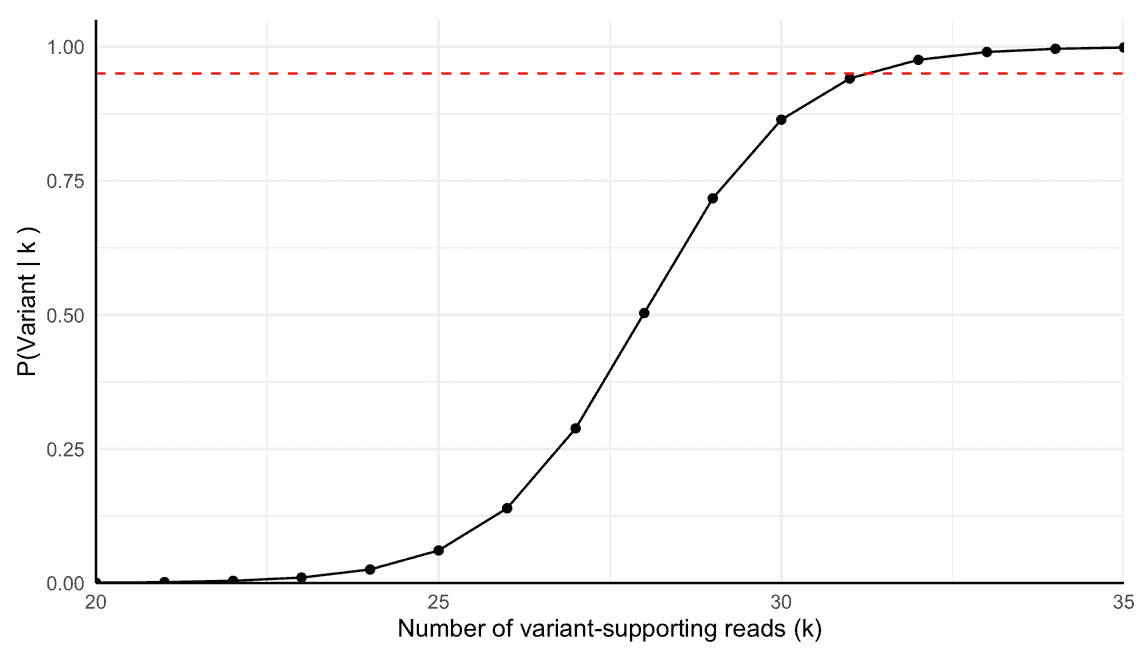
In this section we have seen how the number of reads needed to detect a variant at a given frequency can be calculated using Bayes’ theorem and the binomial distribution. We calculated the number of reads needed to confidently state a variant is present. This number depends on the variant frequency, the error rate, and the prior probability of a variant being present. In reality, this is a simplification, as the error rate is not constant across the genome, and the prior probability of a variant being present is not always known. There may be other complicating factors such as errors in reads not being independent or the presence of multiple variants.

Summary

In this article, we explored the fundamental mathematical principles behind variant calling, focusing on the limitations imposed by sequencing error rates and low variant allele frequencies. Using Bayes’ theorem and binomial models, we showed that observing the expected number of variant-supporting reads may not provide strong evidence for a true variant, especially when prior probabilities are low and error rates are comparable to variant frequencies. This highlights the importance of understanding not just the presence of supporting reads, but the statistical confidence we can assign to those observations.

We demonstrated that a seemingly intuitive threshold, such as 0.3% variant-supporting reads implying a 0.3% VAF, can be misleading. Instead, confidence in a variant call depends on multiple factors: the number of reads, the sequencing error rate, the expected variant frequency, and prior belief in the presence of a variant. We also introduced a general formula to estimate how many reads are needed to detect a variant at a given frequency with a specified level of confidence.

In part 2 of this series, we will extend this mathematical framework to evaluate the performance of variant callers. We’ll explore how the concepts of precision (how often variant calls are correct) and recall (how often true variants are detected) emerge from this statistical foundation, and how to use these metrics to make informed decisions in practical genomics workflows.